Theory crash course

The R package pcpr implements Principal Component Pursuit (PCP), a robust dimensionality reduction technique, for pattern recognition tailored to environmental health (EH) data. The statistical methodology and computational details are provided in Gibson et al. (2022).

In this code-free vignette, we present a crash course in PCP’s theoretical background, so researchers can better navigate all of the functionality offered in pcpr. We will touch upon:

1. PCP’s modeling overview
2. The low-rank and sparse matrices L and S
3. The EH-specific extensions in pcpr
4. Convex and non-convex PCP
5. PCP parameters lambda, mu, and eta
6. Tuning parameters with grid_search_cv()

We recommend users skim this crash course before reading the two code-heavy vignettes:

• vignette("pcp-quickstart"): applying PCP to a simulated environmental mixture
• vignette("pcp-applied"): employing PCP for source apportionment of real-world PM2.5 air pollution concentration data using the queens dataset

PCP modeling overview

PCP algorithms model an observed exposure matrix \(D\) as the sum of three underlying ground-truth matrices:

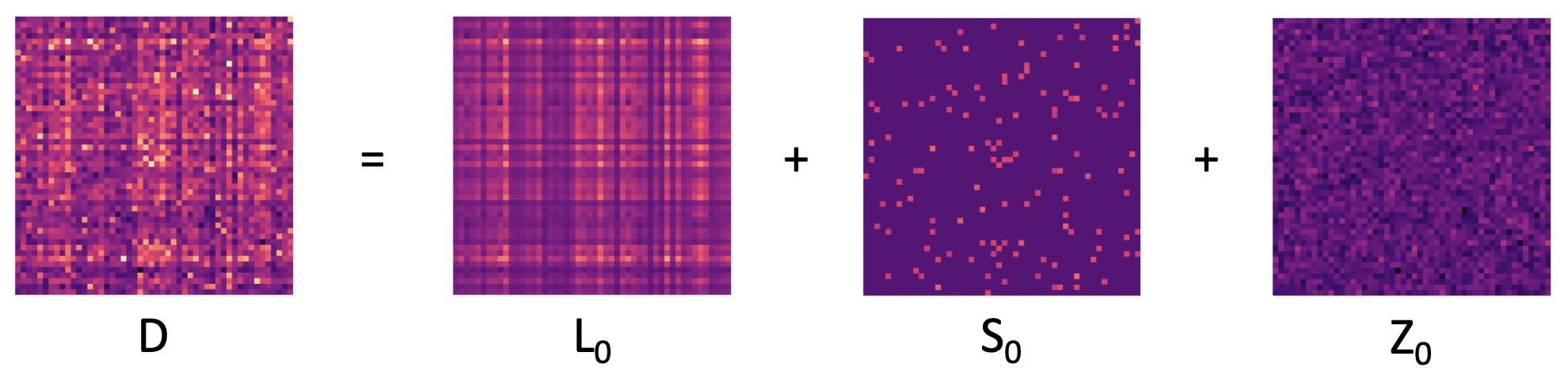
a low-rank matrix \(L_0\) encoding consistent patterns of exposure, a sparse matrix \(S_0\) isolating unique or outlying exposure events (that cannot be explained by the consistent exposure patterns), and dense noise \(Z_0\). All of these matrices are of dimension \(n \times p\), where \(n\) is the number of observations (e.g. study participants or measurement dates) and \(p\) is the number of exposures (e.g. chemical and/or non-chemical stressors). Beyond this mixtures model, the main assumption made by PCP is that \(Z_0 \sim N(\mu, \sigma^2)\) consists of independently and identically distributed (i.i.d.) Gaussian noise corrupting each entry of the overall exposure matrix \(D\).

The models in pcpr seek to decompose an observed data matrix \(D\) into estimated low-rank and sparse components \(L\) and \(S\) for use in downstream environmental health analyses.

The low-rank matrix

The estimated low-rank matrix \(L\) provides information on the consistent exposure patterns, satisfying:

\[r = \text{rank}(L) \ll \min(n, p).\]

The rank \(r\) of a matrix is the number of linearly independent columns or rows in the matrix, and plays an important role in defining the mathematical structure of the data. Intuitively, the rank directly corresponds to the (relatively few) number of underlying patterns governing the mixture. Here, “patterns” can refer to specific sources, profiles or behaviors leading to exposure, depending on the application.

Contrary to closely related dimension reduction tools such as principal component analysis (PCA), PCP infers the rank \(r\) from the observed data. In pcpr, this is done directly during optimization for convex PCP, and via grid search for non-convex PCP. As such, rather than require the researcher to choose the number of estimated patterns for use in subsequent health models, PCP allows the observed data to “speak for itself”, thereby removing potential points of subjectivity in model design.

Notice that \(L \in \mathbb{R}^{n \times p}\), meaning it is still defined in terms of the original \(n\)-many observations and \(p\)-many environmental variables. Put differently, \(L\) can be taken as a robust approximation to the true environmental mixture matrix, unperturbed by outliers (captured in \(S\)) or noise (handled by PCP’s noise term). In this way, the latent exposure patterns are encoded in \(L\) rather than directly estimated. To explicitly obtain the exposure patterns from \(L\), PCP may then be paired with various matrix factorization methods (e.g., PCA, factor analysis, or non-negative matrix factorization) that yield chemical loadings and individual scores for use in downstream health models.

This flexibility allows \(L\) to adapt to mixture-specific assumptions. For example, if the assumption of orthogonal (i.e., independent) patterns is too strong, then instead of pairing \(L\) with PCA, a more appropriate method such as factor analysis can be used. Alternatively, depending on the sample size and study design, \(L\) may also be directly incorporated into regression models.

The sparse matrix

The estimated sparse matrix \(S\) captures unusually high or low outlying exposure events, unexplained by the identified patterns in \(L\). Most entries in \(S\) are 0, with non-zero entries identifying such extreme exposure activity. The number, location (i.e., support), and value of non-zero entries in \(S\) need not be a priori defined; PCP isolates these itself during optimization.

By separating and retaining sparse exposure events, PCP boasts an enormous advantage over other current dimension reduction techniques. Despite being common phenomena in mixtures data, sparse outliers are typically removed from the exposure matrix prior to analysis. This is because PCA and other conventional dimension reduction approaches are unable to disentangle such unique events from the overall patterns of exposure: If included, even low fractions of outliers can deviate patterns identified by traditional methods away from the true distribution of the data, yielding inaccurate pattern estimations and high false positive rates of detected outliers. By decomposing a mixture into low-rank and sparse components \(L\) and \(S\), PCP avoids such pitfalls.

Extensions for environmental health data

The functions in pcpr are outfitted with three environmental health (EH)-specific extensions, making pcpr particularly powerful for EH research:

1. Missing value functionality: PCP is able to recover NA values in the observed mixture matrix, often outperforming traditional imputation techniques.
2. Leveraging potential limit of detection (LOD) information: When equipped with LOD information, PCP treats any estimations of values known to be below the LOD as equally valid if their approximations fall between 0 and the LOD. PCP with LOD data often outperforms PCA imputed with \(\frac{LOD}{\sqrt{2}}\).
3. Non-negativity constraint on the estimated L matrix: If desired, PCP can enforce values in the estimated low-rank matrix L to be \(\geq 0\), better modeling real world mixtures data.

Missing value functionality

PCP assumes that the same data generating mechanisms govern both the missing and the observed entries in \(D\). Because PCP primarily seeks accurate estimation of patterns rather than individual observations, this assumption is reasonable, but in some edge cases may not always be justified. Missing values in \(D\) are therefore reconstructed in the recovered low-rank \(L\) matrix according to the underlying patterns in \(L\). There are three corollaries to keep in mind regarding the quality of recovered missing observations:

1. Recovery of missing entries in \(D\) relies on accurate estimation of \(L\);
2. The fewer observations there are in \(D\), the harder it is to accurately reconstruct \(L\) (therefore estimation of both unobserved and observed measurements in \(L\) degrades); and
3. Greater proportions of missingness in \(D\) artificially drive up the sparsity of the estimated \(S\) matrix. This is because it is not possible to recover a sparse event in \(S\) when the corresponding entry in \(D\) is unobserved. By definition, sparse events in \(S\) cannot be explained by the consistent patterns in \(L\). Practically, if 20% of the entries in \(D\) are missing, then at least 20% of the entries in \(S\) will be 0.

Leveraging potential limit of detection (LOD) information

When equipped with \(LOD\) information, PCP treats any estimations of values known to be below the \(LOD\) as equally valid if their approximations fall between \(0\) and the \(LOD\). Over the course of optimization, observations below the LOD are pushed into this known range \([0, LOD]\) using penalties from above and below: should a \(< LOD\) estimate be \(< 0\), it is stringently penalized, since measured observations cannot be negative. On the other hand, if a \(< LOD\) estimate is \(> LOD\), it is also heavily penalized: less so than when \(< 0\), but more so than observations known to be above the \(LOD\), because we have prior information that these observations must be below \(LOD\). Observations known to be above the \(LOD\) are penalized as usual, using the Frobenius norm in the above objective function.

Gibson et al. (2022) demonstrate that in experimental settings with up to 50% of the data corrupted below the \(LOD\), PCP with the \(LOD\) extension boasts superior accuracy of recovered \(L\) models compared to PCA coupled with \(\frac{LOD}{\sqrt{2}}\) imputation. PCP even outperforms PCA in low-noise scenarios with as much as 75% of the data corrupted below the \(LOD\). The few situations in which PCA bettered PCP were those pathological cases in which \(D\) was characterized by extreme noise and huge proportions (i.e., 75%) of observations falling below the \(LOD\).

Non-negativity constraint on the estimated L matrix

To enhance interpretability of PCP-rendered solutions, there is an optional non-negativity constraint that can be imposed on the \(L\) matrix to ensure all estimated values within it are \(\geq 0\). This prevents researchers from having to deal with negative observation values and questions surrounding their meaning and utility. Non-negative \(L\) models also allow for seamless use of methods such as non-negative matrix factorization to extract non-negative patterns.

Currently, the non-negativity constraint is only supported in the convex PCP function root_pcp(), incorporated in the ADMM splitting technique via the introduction of an additional optimization variable and corresponding constraint. Future work will extend the constraint to the non-convex PCP method rrmc().

Convex vs. non-convex PCP

Of the many flavors of PCP undergoing active study in the current literature, we provide two distinct models in pcpr: the convex model root_pcp() and non-convex model rrmc(). The table below offers a quick glance at their relative differences:

	root_pcp()	rrmc()
Convex?	Yes	No
Convergence?	Slow	Fast
Expected low-rank structure?	Well-defined	Complex
Parameters?	\(D, \lambda, \mu\)	\(D, r, \eta\)
Supports missing values?	Yes	Yes
Supports LOD penalty?	Yes	Yes
Supports non-negativity constraint?	Yes	No
Rank determination?	Autonomous	User-defined*
Sparse event identification?	Autonomous	Autonomous
Optimization approach?	ADMM	Iterative rank-based

*rrmc() can be paired with the cross-validated grid_search_cv() function for autonomous rank determination.

Convex PCP via root_pcp() is best for data characterized by rapidly decaying singular values (e.g. image and video data), indicative of very well-defined latent patterns.

Non-convex PCP with rrmc() is best suited for data characterized by slowly decaying singular values, indicative of complex underlying patterns and a relatively large degree of noise. Most EH data can be described this way, so we expect most EH researchers to utilize rrmc() in their analyses, however there are cases where the convexity of root_pcp() may be preferable.

Convex PCP

Convex PCP formulations possess a number of particularly attractive properties, foremost of which is convexity, meaning that every local optimum is a global optimum, and a single best solution exists. Convex approaches to PCP also have the virtue that the rank \(r\) of the recovered \(L\) matrix is determined during optimization, without researcher input.

Unfortunately, these benefits come at a cost: convex PCP programs are expensive to run on large datasets, suffering from poor convergence rates. Moreover, convex PCP approaches are best suited to instances in which the target low-rank matrix \(L_0\) can be accurately modelled as low-rank (i.e. \(L_0\) is governed by only a few very well-defined patterns). This is often the case with image and video data (characterized by rapidly decaying singular values), but not common for EH data. EH data is typically only approximately low-rank (characterized by complex patterns and slowly decaying singular values).

The convex model available in pcpr is root_pcp(). For a comprehensive technical understanding, we refer readers to Zhang et al. (2021) introducing the algorithm.

root_pcp() optimizes the following objective function:

\[\min_{L, S} ||L||_* + \lambda ||S||_1 + \mu ||L + S - D||_F\]

The first term is the nuclear norm of the L matrix, incentivizing \(L\) to be low-rank. The second term is the \(\ell_1\) norm of the S matrix, encouraging S to be sparse. The third term is the Frobenius norm applied to the model’s noise, ensuring that the estimated low-rank and sparse models \(L\) and \(S\) together have high fidelity to the observed data \(D\). The objective is not smooth nor differentiable, however it is convex and separable. As such, it is optimized using the Alternating Direction Method of Multipliers (ADMM) algorithm (Boyd et al. (2011)), (Gao et al. (2020)).

Non-convex PCP

To alleviate the high computational complexity of convex methods, non-convex PCP frameworks have been developed. These drastically improve upon the convergence rates of their convex counterparts. Better still, non-convex PCP methods more flexibly accommodate data lacking a well-defined low-rank structure, so they are from the outset better suited to handling EH data. Non-convex formulations provide this flexibility by allowing the user to interrogate the data at different ranks.

The drawback here is that non-convex algorithms can no longer determine the rank best describing the data on their own, instead requiring the researcher to subjectively specify the rank \(r\) as in PCA. However, by pairing non-convex PCP algorithms with the cross-validation routine implemented in the grid_search_cv() function, the optimal rank can be determined semi-autonomously; the researcher need only define a rank search space from which the optimal rank will be identified via grid search. One of the more glaring trade-offs made by non-convex methods for this improved run-time and flexibility is weaker theoretical promises; specifically, non-convex PCP runs the risk of finding spurious local optima, rather than the global optimum guaranteed by their convex siblings. Having said that, theory has been developed guaranteeing equivalent performance between non-convex implementations and closely related convex formulations under certain conditions. These advancements provide strong motivation for non-convex frameworks despite their weaker theoretical promises.

The non-convex model available in pcpr is rrmc(). We refer readers to Cherapanamjeri et al. (2017) for an in depth look at the mathematical details.

rrmc() implicitly optimizes the following objective function:

\[\min_{L, S} I_{rank(L) \leq r} + \eta ||S||_0 + ||L + S - D||_F^2\]

The first term is the indicator function checking that the \(L\) matrix is strictly rank \(r\) or less, implemented using a rank \(r\) projection operator proj_rank_r(). The second term is the \(\ell_0\) norm applied to the \(S\) matrix to encourage sparsity, and is implemented with the help of an adaptive hard-thresholding operator hard_threshold(). The third term is the squared Frobenius norm applied to the model’s noise.

rrmc() uses an incremental rank-based strategy in order to estimate \(L\) and \(S\): First, a rank-\(1\) model \((L^{(1)}, S^{(1)})\) is estimated. The rank-\(1\) model is then used as an initialization point to construct a rank-\(2\) model \((L^{(2)}, S^{(2)})\), and so on, until the desired rank-r model \((L^{(r)}, S^{(r)})\) is recovered. All models from ranks \(1\) through \(r\) are returned by rrmc() in this way.

PCP parameters

Intuition behind lambda, mu, and eta

Recall root_pcp()’s objective function is given by:

\[\min_{L, S} ||L||_* + \lambda ||S||_1 + \mu ||L + S - D||_F\]

• \(\lambda\) (lambda) controls the sparsity of root_pcp()’s output \(S\) matrix; larger values of \(\lambda\) penalize non-zero entries in \(S\) more stringently, driving the recovery of sparser \(S\) matrices. Therefore, if you a priori expect few outlying events in your model, you might expect a grid search to recover relatively larger \(\lambda\) values, and vice-versa.
• \(\mu\) (mu) adjusts root_pcp()’s sensitivity to noise; larger values of \(\mu\) penalize errors between the predicted model and the observed data (i.e. noise), more severely. Environmental data subject to higher noise levels therefore require a root_pcp() model equipped with smaller mu values (since higher noise means a greater discrepancy between the observed mixture and the true underlying low-rank and sparse model). In virtually noise-free settings (e.g. simulations), larger values of \(\mu\) would be appropriate.

rrmc()’s objective function is given by:

\[\min_{L, S} I_{rank(L) \leq r} + \eta ||S||_0 + ||L + S - D||_F^2\]

• \(\eta\) (eta) controls the sparsity of rrmc()’s output \(S\) matrix, just as \(\lambda\) does for root_pcp(). Because there are no other parameters scaling the noise term, \(\eta\) can be thought of as a ratio between root_pcp()’s \(\lambda\) and \(\mu\): Larger values of \(\eta\) will place a greater emphasis on penalizing the non-zero entries in \(S\) over penalizing the errors between the predicted and observed data (the dense noise \(Z\)).

Theoretically optimal parameters

The get_pcp_defaults() function calculates the “default” PCP parameter settings of \(\lambda\), \(\mu\) and \(\eta\) for a given data matrix \(D\).

The “default” values of \(\lambda\) and \(\mu\) offer theoretical guarantees of optimal estimation performance. Candès et al. (2011) obtained the guarantee for \(\lambda\), while Zhang et al. (2021) obtained the result for \(\mu\). It has not yet been proven whether or not \(\eta\) enjoys similar properties.

The theoretically optimal \(\lambda_*\) is given by:

\[\lambda_* = 1 / \sqrt{\max(n, p)},\]

where \(n\) and \(p\) are the dimensions of the input matrix \(D_{n \times p}\).

The theoretically optimal \(\mu_*\) is given by: \[\mu_* = \sqrt{\frac{\min(n, p)}{2}}.\]

The “default” value of \(\eta\) is then simply \(\eta = \frac{\lambda_*}{\mu_*}\).

Empirically optimal parameters

Mixtures data is rarely so well-behaved in practice, however. Instead, it is common to find different empirically optimal parameter values after tuning these parameters in a grid search. Therefore, it is recommended to use get_pcp_defaults() primarily to help define a reasonable initial parameter search space to pass into grid_search_cv().

Tuning parameters with grid_search_cv()

Cross-validation procedure

grid_search_cv() conducts a Monte Carlo style cross-validated grid search of PCP parameters for a given data matrix \(D\), PCP function pcp_fn, and grid of parameter settings to search through grid. The run time of the grid search can be sped up using bespoke parallelization settings.

Each hyperparameter setting is cross-validated by:

1. Randomly corrupting \(\xi\) percent of the entries in \(D\) as missing (i.e. NA values), yielding \(P_\Omega(D)\). Done using the sim_na() function.
2. Running the given PCP function pcp_fn on \(P_\Omega(D)\), yielding estimates \(L\) and \(S\).
3. Recording the relative recovery error of \(L\) compared with the input data matrix \(D\) for only those values that were imputed as missing during the corruption step (step 1 above). Formally, the relative error is calculated with: \[RelativeError(L | D) := \frac{||P_{\Omega^c}(D - L)||_F}{||P_{\Omega^c}(D)||_F}\]
4. Re-running steps 1-3 for a total of \(K\)-many runs (each “run” has a unique random seed from 1 to \(K\) associated with it).
5. Performance statistics can then be calculated for each “run”, and then summarized across all runs using mean-aggregated statistics.

In the grid_search_cv() function, \(\xi\) is referred to as perc_test (percent test), while \(K\) is known as num_runs (number of runs).

Best practices for \(\xi\) and \(K\)

Experimentally, this grid search procedure retrieves the best performing PCP parameter settings when \(\xi\) is relatively low, e.g. \(\xi = 0.05\), or 5%, and \(K\) is relatively high, e.g. \(K = 100\). This is because:

• The larger \(\xi\) is, the more the test set turns into a matrix completion problem, rather than the desired matrix decomposition problem. To better resemble the actual problem PCP will be faced with come inference time, \(\xi\) should therefore be kept relatively low.
• Choosing a reasonable value for \(K\) is dependent on the need to keep \(\xi\) relatively low. Ideally, a large enough \(K\) is used so that many (if not all) of the entries in \(D\) are likely to eventually be tested. Note that since test set entries are chosen randomly for all runs \(1\) through \(K\), in the pathologically worst case scenario, the same exact test set could be drawn each time. In the best case scenario, a different test set is obtained each run, providing balanced coverage of \(D\). Viewed another way, the smaller \(K\) is, the more the results are susceptible to overfitting to the relatively few selected test sets.

Interpretation of results

Once the grid search of has been conducted, the optimal hyperparameters can be chosen by examining the output statistics summary_stats. Below are a few suggestions for how to interpret the summary_stats table:

• Generally speaking, the first thing a user will want to inspect is the rel_err statistic, capturing the relative discrepancy between recovered test sets and their original, observed (yet possibly noisy) values. Lower rel_err means the PCP model was better able to recover the held-out test set. So, in general, the best parameter settings are those with the lowest rel_err. Having said this, it is important to remember that this statistic should be taken with a grain of salt: Because in practice the researcher does not have access to the ground truth \(L\) matrix, the rel_err measurement is forced to rely on the comparison between the noisy observed data matrix \(D\) and the estimated low-rank model \(L\). So the rel_err metric is an “apples to oranges” relative error. For data that is a priori expected to be subject to a high degree of noise, it may actually be better to discard parameter settings with suspiciously low rel_errs (in which case the solution may be hallucinating an inaccurate low-rank structure from the observed noise).
• For grid searches using root_pcp() as the PCP model, parameters that fail to converge can be discarded. Generally, fewer root_pcp() iterations (num_iter) taken to reach convergence portend a more reliable / stable solution. In rare cases, the user may need to increase root_pcp()’s max_iter argument to reach convergence. rrmc() does not report convergence metadata, as its optimization scheme runs for a fixed number of iterations.
• Parameter settings with unreasonable sparsity or rank measurements can also be discarded. Here, “unreasonable” means these reported metrics flagrantly contradict prior assumptions, knowledge, or work. For instance, most air pollution datasets contain a number of extreme exposure events, so PCP solutions returning sparse \(S\) models with 100% sparsity have obviously been regularized too heavily. Note that reported sparsity and rank measurements are estimates heavily dependent on the thresh set by the sparsity() & matrix_rank() functions. E.g. it could be that the actual average matrix rank is much higher or lower when a threshold that better takes into account the relative scale of the singular values is used. Likewise for the sparsity estimations. Also, recall that the given value for \(\xi\) artifically sets a sparsity floor, since those missing entries in the test set cannot be recovered in the \(S\) matrix. E.g. if \(\xi = 0.05\), then no parameter setting will have an estimated sparsity lower than 5%.

Coded example analyses

To see how to apply all of the above in pcpr, we recommend reading:

• vignette("pcp-quickstart"): applying PCP to a simulated environmental mixture
• vignette("pcp-applied"): employing PCP for source apportionment of real-world PM2.5 air pollution concentration data using the queens dataset

References

Gibson, Elizabeth A., Junhui Zhang, Jingkai Yan, Lawrence Chillrud, Jaime Benavides, Yanelli Nunez, Julie B. Herbstman, Jeff Goldsmith, John Wright, and Marianthi-Anna Kioumourtzoglou. “Principal component pursuit for pattern identification in environmental mixtures.” Environmental Health Perspectives 130, no. 11 (2022): 117008.

Zhang, Junhui, Jingkai Yan, and John Wright. “Square root principal component pursuit: tuning-free noisy robust matrix recovery.” Advances in Neural Information Processing Systems 34 (2021): 29464-29475.

Boyd, Stephen, Neal Parikh, Eric Chu, Borja Peleato, and Jonathan Eckstein. “Distributed optimization and statistical learning via the alternating direction method of multipliers.” Foundations and Trends in Machine learning 3, no. 1 (2011): 1-122.

Gao, Wenbo, Donald Goldfarb, and Frank E. Curtis. “ADMM for multiaffine constrained optimization.” Optimization Methods and Software 35, no. 2 (2020): 257-303.

Cherapanamjeri, Yeshwanth, Kartik Gupta, and Prateek Jain. “Nearly optimal robust matrix completion.” International Conference on Machine Learning. PMLR, 2017.

Candès, Emmanuel J., Xiaodong Li, Yi Ma, and John Wright. “Robust principal component analysis?.” Journal of the ACM (JACM) 58, no. 3 (2011): 1-37.